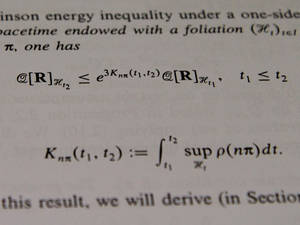Relativitätstheorie zu Ende gedacht

Stellt man sich das Universum als Kunstwerk vor, so gibt es zwei Größen, die es modellieren: "der Raum", also unser tatsächliches Lebensumfeld - und dessen zeitliche Entwicklung, "die Zeit". Die "Raumzeit" kennt einen genialen Künstler: Albert Einstein hat 1905 mit der Speziellen Relativitätstheorie und 1916 mit der Allgemeinen Relativitätstheorie den wissenschaftlichen Kosmos revolutioniert. Einsteins Gleichungen gelten heute als Basis unseres Weltverständnisses – sie lassen etwa die Erklärung der Gravitation durch die Krümmung der Raumzeit zu und ermöglichen damit unter anderem die mathematische Beschreibung von "Kunstwerken" wie Sternen und Schwarzen Löchern.

Die Vermessung des Universums

Es klingt ein bisschen nach "Vermessung des Universums", wenn Annegret Burtscher vom Institut für Mathematik der Universität Wien über ihr differentialgeometrisches Forschungsprojekt zur Allgemeinen Relativitätstheorie erzählt. "Die Existenz von Lösungen ist gesichert", so die junge Mathematikerin, "ihr Verhalten aber nur teilweise bekannt." Burtscher, die ihre Leidenschaft für die Einstein-Gleichungen im Rahmen einer Lehrveranstaltung über Differentialgeometrie entdeckte, untersucht, "was mit Lösungen der Einstein-Gleichungen passiert, wenn man sie über einen längeren Zeitraum untersucht. Taucht eine Singularität auf, oder kann man die Lösung beliebig lang fortsetzen – besitzt sie also globale, unendliche Gültigkeit?"

Die Nadel am Luftballon

Was abstrakt anmutet, veranschaulicht die Wissenschafterin, die 2012 das L'Oréal Österreich Stipendium "For Women in Science" erhalten hat, an einem Beispiel: "Stellt man sich vor, man bläst einen Luftballon auf, so gibt es zwei Möglichkeiten: Entweder der Luftballon zerplatzt, oder er wird unendlich groß – wie das expandierende Universum. Berührt man nun die Oberfläche des Luftballons mit einer Nadel, krümmt sich der Luftballon – unter Umständen so lange, bis er platzt. Das Raum-Zeit-Gefüge würde also nicht mehr funktionieren." Ihre Fragestellung könnte man also so übersetzen: Gibt es eine Nadel am Luftballon? Und wenn ja: Wo und in welcher Form ist sie wirksam?

Die Zukunft erfassbar machen

In ihrem Dissertationsprojekt wagt die Mathematikerin einen Blick in die Zukunft. Sie prüft, wie sich die Gleichungen unter verschiedenen Bedingungen verhalten. Abhängig von den gewählten Anfangswerten können die Lösungen variieren: Bewegen sich die Anfangswerte in einem bestimmten Bereich, bleiben die Lösungen bestehen. "Unter Umständen lassen sich aber konkrete Bedingungen festmachen, unter denen die Lösungen nicht mehr gültig sind", so die Forscherin.

Einstein-Gleichungen neu

Erste Publikationen im Rahmen des Dissertationsprojekts von Annegret Burtscher zeigen spannende Ergebnisse, etwa bezüglich der Abschätzung der Bel-Robinson-Energie, die bei der Untersuchung des globalen Verhaltens von Raumzeiten eine wichtige Rolle spielt. Mehrere vielbeachtete Papers, die an der Universität Wien und bei Forschungsaufenthalten in Paris entstanden sind, stießen auf großes Interesse in der Scientific Community. Als Mathematikerin liefert Burtscher damit theoretische Modelle, die etwa für die Astronomie, Astrophysik und Kosmologie bedeutsam sind. Ein allgegenwärtiges Anwendungsgebiet der Relativitätstheorie ist beispielsweise die GPS-Technologie, bei der die Berechnung der korrekten Laufzeit zwischen Erde und Satelliten maßgeblich von relativistischen Effekten abhängig ist.

	Das abgebildete Theorem beschreibt die Abschätzung der Bel-Robinson-Energie. Es besagt, dass die Energie zum Zeitpunkt t2 abhängig von einem bestimmten Faktor durch die Energie zum einem früheren Zeitpunkt t1 abschätzbar ist. Neue Erkenntnisse von Annegret Burtscher zeigen: Um den Faktor einschätzen zu können, ist nur eine einseitige Beschränkung der Krümmung notwendig.

 
Mathematik zwischen Universität und Familie

Vom "Einstein-Image" des zerstreuten, zerzausten Professors ist die junge Mathematikerin Annegret Burtscher weit entfernt. Privat versucht sie, ihre Familie – "mein Mann ist ebenfalls Mathematiker, und wir haben eine kleine Tochter" –, und ihren leidenschaftlichen Forscherdrang unter einen Hut zu bringen. Dass wissenschaftliche Führungspositionen in der Mathematik überwiegend mit Männern besetzt sind, dass die Kinderbetreuung etwa bei Auslandsaufenthalten und Konferenzen problematisch ist und das Berufsbild "Mathematikerin" noch nicht vollständig gesellschaftlich etabliert ist, bestärkt Annegret Burtscher in ihrer Vorbildfunktion: "Man braucht Durchhaltevermögen und Inspiration. Das möchte ich im universitären Alltag und in meinen Lehrveranstaltungen vermitteln."

Aufbauend auf ihrer Dissertation verfolgt die zielstrebige Jungwissenschafterin einen interdisziplinär orientierten Weg: Sie will Analysis und Differentialgeometrie mit anderen Disziplinen wie der Physik und den Erdwissenschaften verknüpfen und "an deren Schnittmenge den Blick für Verbindungen von Theorien schärfen." (sb)

Annegret Burtscher realisiert ihr Dissertationsprojekt mit Unterstützung des L’ORÉAL Österreich Stipendiums "For Women in Science". In ihrer mathematischen Auseinandersetzung mit der Allgemeinen Relativitätstheorie beschäftigt sie sich mit den geometrischen Abbruchbedingungen von Lösungen der Einstein-Gleichungen. Die geometrische Seite ihrer Arbeit ist an der Fakultät für Mathematik der Universität Wien, die analytische an der Université Pierre et Marie Curie in Paris angesiedelt.